|
段文泽1 林 涛2 段 鹰3
(1.2. 重庆大学电气工程学院, 重庆 400044; 3. 重庆大学机械工程学院 ,重庆 400044)
摘要:作者以系统方法论为指导,已有研究工作为素材,分析大系统建模中如何实现宏观与微观、经验与理论、定性与定量的辨证统一。归纳了几种具体集成模式,包括宏观统计机理模型、关联过程协调模型和智能参数修正模型。从其中进一步提出了一些建模的指导思想。
关键词:大系统建模,方法论,系统集成模式,建模指导思想
中图分类号: N945.12 文献标识码: A
Groping for Methodology on Large Scale System Modeling
DUAN Wenze1, LIN Tao2 , DUAN Ying3
(1.2.College of Electrical Engineering, Chongqing University ,Chongqing 400044,China;
3. College of Mechanical Engineering, Chongqing University, Chongqing 400044, China)
Abstract: Under the guidance of system methodology, the problem how to realize the dialectic unification of macroscopic and microcosmic, experience and theory, qualitative and quantitative in large scale system modeling is analyzed by material of the existing research. Several incorporate modes, including macroscopic statistic mechanical model, harmonious model of correlative process and intelligent correctional parameter model, have been concluded. Some guidelines of modeling have been farther advanced.
Key words: Large scale system modeling, Methodology, Incorporate modes of system, Guidelines of modeling
CLC Numbers: N945.12 Document Code: A
1 引言
科学发展经历了三个阶段:古代缺乏精确的量测和实验手段,对客观世界无法进行深入研究,只能从总体上观察、猜测和思考,这就是总体思辩阶段。亚里斯多德等古希腊思想家都强调总体观,提出“总体功能可大于它各部分功能的总和”这一系统论的基本原理。中国古代的《周易》、《老子》等也强调部分之间、部分与整体之间、整体与环境之间的相互联系及整体的协调性,中医提倡辨证施治,反对“头痛医头脚痛医脚”。这些科学观至今仍闪耀光辉。但是,由于缺乏对细节的解剖与观测,只能用猜测和思辩补充,限制了科学技术的快速发展。从15世纪末到19世纪是科学形成和大发展的阶段。人们开始深入事物内部,对其逐次分解,分类研究,产生了数学、物理学、化学、天文学、生物学等近代科学,它们从统一的哲学中分离出来,自成体系,越分越细。强调分解的还原论和拉普拉斯决定论是这一时期方法论的代表。它与古代的总体思辩相比是一个进步,促进了各种具体精细知识的积累,促成了伟大的工业革命。20 世纪以来,科学进入了现代发展阶段,还原论妨碍科学发展和技术进步的特征开始体现出来。贝塔朗菲发现,在生物学研究中,解剖已从肌肉、血管、神经进入分子的层次,但把这些细微知识机械相加仍不能解决问题,甚至分的越细,越失去全貌。他认识到只有把生物作为一个有机整体并和其所处环境作为一个大系统来研究,才能解决问题,由此开创了理论生物学。随着生产规模的扩大化和生产过程的复杂化,在工程技术领域也发生了类似的情况。人们的认识又回到了整体观,但它已不是古代的总体思辩,而是经过还原和分解研究之后的整体协调。这是一个更大的进步。人们的认识就是这样螺旋上升的。
钱学森等总结了这一认识上的飞跃,提出还原论和整体轮的辨证统一是研究复杂大系统和巨系统的正确方法论,即系统方法论[1]。他还进一步提出,还原的细化应适可而止,整体的扩大也应恰到好处。这一方面是受人们认识局限性约束,另一方面也是为了抓住问题的主要矛盾,该指导思想符合辨证法。科学发展史上出现过背离辨证法的倾向:一提还原就忘了整体,一提整体又丢弃还原,结果都遭失败。如何将还原论和整体论辨证统一,即如何处理局部与整体、微观与宏观、经验和理论、定性与定量、感性与理性等问题,成了系统方法论的核心问题。这实质上是建模问题。对复杂大系统或巨系统,钱学森提出定性到定量的综合集成法,具有一定普适性。但具体问题终究千差万别,辨证统一往往表现为多种形态。归纳同类性质问题,提出适当的方法和指导思想,将使方法论更为丰富。
现有建模方法大体可分为白箱、黑箱和灰箱模型。白箱模型是根据系统运动规律建立的“机理模型”,它提供较完整的信息,在机理清楚的情况采用。黑箱模型一般是输入输出模型,可用统计或智能方法(如神经网络)建立,它无法反映系统的内部状态,在机理不清楚时采用。如果我们对系统的结构和机理掌握部分知识,应充分利用,将黑箱转化为灰箱,提供更多的信息。但是这一结论并不绝对,如果我们对系统某些状态不感兴趣,也可略去这部分机理知识。灰箱模型是在工程中遇到最多的情况,建模方法各有差异。本文总结作者在大系统建模与控制中的若干方法,提出若干建模的指导思想,作为对方法论的探索。
2 宏观统计—机理模型
存在这样一类大系统,其微观机理清楚但系统结构参数不确知,宏观机理不清楚但掌握运行统计数据,城市复杂供水系统就是一例,它的网孔成百上千,节点成千上万。若是将系统还原到这些网孔和节点来建立其运动方程,将遇到“维数灾”,何况深埋地下的管网一般情况不明,问题具有“不确知性”。从运行经验看,经过平差的管网,只要对少数监控点运行参数加以测控,就能使全网满意运行。据此,Demoyer建立了管网宏观统计模型[2],这是一个回归系数无物理意义的黑箱模型,不能反映管网内部状态并估计节点流量,使用水量的分时分地预报无法进行,难以更好实现管网的优化调度。建立宏观模型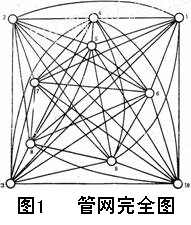 缺乏机理知识是问题的焦点,但仔细分析也并非完全缺乏,其大体结构还是知道的。我们原则上可以根据管网的最小单位来合成系统,对线性网络,通过串并联等效变换、星-角变换或多射线星型-等值多边型变换可逐步减少节点的数目,最后只保留少量监控点。实际建模时,不需也不可能逐一进行上述繁琐变换,只要按N个监控点构成完全图即可,完全图的边具有管路特性,如图1所示。在相关分析基础上去掉弱相关的边还可简化完全图。对简化图各个边赋以相应物理量,就得等价管网结构图。再列写水力学方程就建立了相应模型[3]。 缺乏机理知识是问题的焦点,但仔细分析也并非完全缺乏,其大体结构还是知道的。我们原则上可以根据管网的最小单位来合成系统,对线性网络,通过串并联等效变换、星-角变换或多射线星型-等值多边型变换可逐步减少节点的数目,最后只保留少量监控点。实际建模时,不需也不可能逐一进行上述繁琐变换,只要按N个监控点构成完全图即可,完全图的边具有管路特性,如图1所示。在相关分析基础上去掉弱相关的边还可简化完全图。对简化图各个边赋以相应物理量,就得等价管网结构图。再列写水力学方程就建立了相应模型[3]。
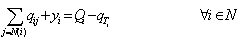 (1) (1)
 (2) (2)
 (3) (3)
这里,等价管网有L个回路,N 个节点,其中W个包括储水池,V个包括泵站。qij是节点i到节点j的管道流量,yi是节点i的集中负荷流量,Qi是泵站输入节点i的流量,qTi是节点i送入储水池的流量,Rij是ij段上的摩阻,U(k)是第k个回路中各支路的集合,xi是储水池水位,S(xi)为储水池横截面积。(1)~(3)式中,Qi 、xi和qTi 是可测量,qij yi 、S(xi)为待辩识量。文[4]详细讨论了这一参数估计问题,文[5]在此基础上首次解决了水负荷的分时分地预报,文[6]更好地解决了优化调度问题。
必须指出,实际网络是非线性的((2)式)。为保证上述变换的有效性,只有在工况小范围变化时进行线性化。具体做法是:取不同天中同一时刻的运行数据来建模,它们之间并无多大差异。据此建立的模型可用于今后同一时刻。这样,一天中有多少个采样时刻,就将建立多少个模型,它们结构一样,参数各异。
由此得到的启示有两点:一是建模工作中切勿轻易放弃有用的机理知识而盲目采用黑箱模型,要针对实际情况具体分析,结合整体论和还原论,不要舍本求末;二是为了宏观与微观的辩证统一,大系统理论中早已定量地采用分解和集成的综合手段,而这里采用的是定性合成(或虚拟合成)与定量分析的综合。该方法把微观机理特性反映到宏观模型中来,解决了节点流量估计问题。这是黑箱模型无法做到的。
3 关联过程协调模型
对于一类生产过程问题,子系统较多,它们通过一个“关联过程”互相影响。关联过程往往是带有时滞作用的物流过程,抓住“关联过程”及相应的“关联变量”来协调各子系统,大系统建模问题就容易解决。生产计划决策系统是典型一例[7],将问题的阶段按计划时间自然划分,阶段周期为T,产出滞后为(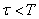 ),其物流平衡方程为 ),其物流平衡方程为
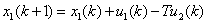 (4) (4)
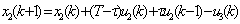 (5) (5)
其中, 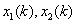 分别为原材料和产品存储量, 分别为原材料和产品存储量,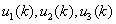 分别为原材料采购量、单位时间投产量和销售量(其中 分别为原材料采购量、单位时间投产量和销售量(其中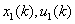 折合为产品量)。生产计划追求整个过程的最大利润,模型如下 折合为产品量)。生产计划追求整个过程的最大利润,模型如下
Mod 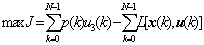 (6) (6)
s.t.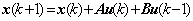 (7) (7)
 (8 ) (8 )
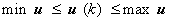 (9) (9)
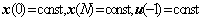 (10) (10)
其中,式(6)等式右端第一项为销售收入,第二项为生产成本,式(7)是(4)、(5)的向量写法。模型结构如图2,图中e(k)、d(k)为原材料采购与存储成本,a(k)、b(k)为开工固定成本和产品生产成本,c(k)为产品存储费,p(k)为产品销售价格。
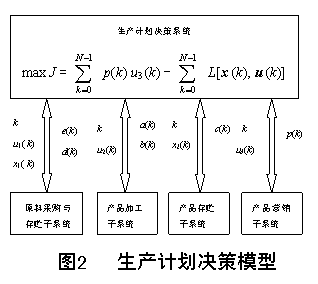
如果关心的是大系统中的某部分,其余子系统的影响机理非常复杂且不确知,则用一“关联过程”代替它们的影响可使问题简化。水厂中,原水从取水泵站送出,经若干水处理环节,到清水池储存(对应于很大纯滞后τ),再由送水泵站送入水网。τ受源水水质与水处理过程影响而产生较大变化。我们不需考虑这些影响的参数和作用机理,只要对τ进行在线辩识并适时修正水量控制模型就可将水质控制过程与水量控制过程解耦。该关联过程为
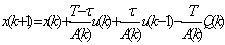 (11) (11)
式中x(k)、A(k)为清水池水位及横截面,u(k)、Q(k)为取水及送水泵站出口流量,T为采样周期。这样式(11)就代替了预沉、投药、混凝、过滤等众多处理过程的影响,直接把取水和送水过程联系起来,简化了问题。将式(11)作为约束条件可建立水量控制的优化控制模型[8]。
从以上讨论得到的启示是:1、整个模型仍是机理模型与统计模型的集成,但问题的关键在于如何根据定性分析确定关联变量,用统计定量分析建立“关联过程模型”;2、根据讨论问题的侧重点,抓住主要矛盾,不必对各复杂因素一一进行机理分析,可用少量或一个关联变量代替其影响,从而简化问题。此时经验往往具有决定作用。
4 智能参数修正模型
有一类系统的过程机理清楚,但若干扰动因素对主要过程的影响机理却不清楚,轧钢加热炉是典型例子。目前有两种思路解决扰动的适应控制问题:一是根据扰动引起的后果采用反馈校正,根据钢坯在初轧机组末端表面温度的偏差值来修正钢温预报模型[9],这种方法简单,但迟延大,实时性差,可能引起振荡;另一个思路在建模时就全面考虑这些扰动因素,由于作用机理不明,只能按多元统计回归理论建立钢温预报模型[10],它能体现更多建模因素的影响,但需用大量计算处理病态数据问题,实时性也差。
在加热炉传热条件(综合辐射热系数c和综合对流热系数h)不变的条件下,完全可以根据机理模型确定炉膛各段温度的优化设定。机理模型不仅在数值上容易处理,符合节省参数的原则,而且可根据已有知识使模型得到适当的简化,使模型参数具有物理意义,保证解的存在性和唯一性。这样辩识的收敛性得到了较好保证,数据的病态问题也降到了最低[11]。机理分析表明,在燃烧控制自寻优的系统中,燃气与空气的流量和压力扰动都反映到炉温T与空燃比r的变化上,这是造成炉膛传热状况变化的主要因素。由于作用机理不明,在试验基础上建立神经网络来描述T、 r与c、h之间的输入输出关系,根据输出来修正模型中的c、h值。把协调级的机理优化模型 [12]与神经网络模型按图3的递阶结构相结合,可达到适应控制的效果。图中,c、h值是缓慢变化的参数,其更新周期应大于燃烧系统的控制周期,Tf(1)…Tf(n)为各段炉温设定,Fa、Ff为空气和燃气流量给定,括号中是相应的反馈量。
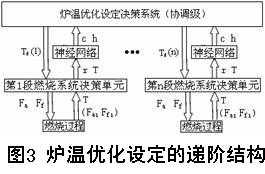
上述方法充分利用了已有的机理知识,部分采用智能模型解决机理不明扰动的影响,其输入量为扰动因素,输出量用来修正机理模型参数,从而实现两种模型的集成。同时考虑了系统中不同因素影响具有不同的时标,其适当处理将利于控制的实时性。
5 结论
系统方法论是大系统建模的指导思想,实践中产生的建模方法经过提炼,反过来又丰富了系统方法论。本文讨论建模中定性与定量的辨证统一,归纳出几种表现形式:宏观统计机理模型、关联过程协调模型和智能参数修正模型。体现的重要思想有:1、先充分利用已有的机理知识,再用黑箱模型补充;2、在某些作用机理不必深究的情况下,可用一简化黑箱模型描述它们的影响;3、为了实现宏观与微观的辩证统一,定性合成与定量分析的综合是有力手段;4、建模中区别变量的缓变和慢变特性是必要的。
参考文献
[1 ] 钱学森. 人体科学与当代科学技术发展纵横观 [M]. 北京:人民出版社,1996.
[2]R.Demoyer,Jr.and Howitz,L.B. Macroscopic Distribution-system Modeling. J. AWWA. July 1975.
[3] 段文泽,刘士荣.城市供水系统建模方法研究[J].系统工程理论与实践,1988,8(3):17-27.
[4] 刘士荣,段文泽.大规模管网系统的有约束参数估计[J].重庆建筑工程学院学报,1987,(3):18-30.
[5]段文泽,刘士荣.城市供水系统负荷量的分时分地预报.中国系统工程学会.发展战略与系统工程[C].北京:学术期刊出版社,1987:573-579.
[6]段文泽,刘士荣.大规模供水系统的动态递阶最优控制[J].系统工程理论与实践,1990,10(6):39-47.
[7] 段鹰,段文泽.大规模时滞系统的动态规划模型与优化算法[J].机械工程学报, 2007,43(4): 217-223.
[8]段文泽,李远树.大系统控制的关联过程协调模型及优化算法[J].系统工程学报,1992, 7(2): 106-115
[9] 王中杰,柴天佑,张莉.加热炉的炉温优化设定模型[J].自动化学报,2000,26(4):465-468.
[10] 梁军.轧钢加热炉钢坯加热质量的检测研究[J].传感技术学报,2003,16(1):59-64
[11] 林涛,段文泽,李昌春.轧钢加热炉建模方法比较研究[J].计算机仿真,2007:待发表.
[12] 段鹰,林涛,段文泽.逆推法实现轧钢加热炉优化控制[J].重庆大学学报,2007,30(8):待发表.
作者简介:段文泽,男,重庆大学教授。从事电气传动自动化、大系统优化控制与人工智能应用等方面的研究。曾任中国自动化学会EA与中国电工技术学会CS委员兼控制理论学组副组长,建设部专家组成员。在国内外高级刊物发表论文50余篇。
通信地址:重庆大学B区东村103-1-2号,邮编:400045。
Email: duanwz35@126.com.
|