部分预应力梁开裂以后截面平均应变和刚度的直接计算法
项剑锋 硕士、教授级高级工程师
(浙江省建筑科学设计研究院、浙江剑锋加固工程有限公司)
提 要:本文基于截面平均应变符合平截面假定,截面弯矩与受拉边缘处平均应变及截面曲率与受拉边缘处平均应变的双折线关系,利用部分预应力梁开裂以后不考虑受拉砼作用时截面上的弯矩—曲率—应变的简化线性关系式,直接导出了开裂以后考虑受拉砼作用时截面平均应变和刚度的精度很高又很简捷的计算公式,并通过计算例题使计算方法更加明了。
关键词:弯矩、曲率、截面平均应变、双折线、刚度、直接计算、计算例题 1 前言
在作预应力梁和钢筋混凝土梁的挠度和裂缝宽度验算时,主要的计算内容是开裂以后的截面平均应变和刚度。由于截面开裂以后,裂缝之间和裂缝顶部的受拉区混凝土还要承担一部分拉力,而这部分拉力的大小和在加荷过程中的衰减速度均受许多因素影响,所以使得开裂以后的截面平均应变和刚度计算变得较为困难。
我国现行混凝土结构设计规范(GB50010-2002)采用将裂缝截面上纵向受拉钢筋的应力(钢筋混凝土梁)或等效应力(预应力混凝土梁)除钢筋弹性模量乘应变不均匀系数的方法计算钢筋重心处的截面平均应变值。裂缝截面上纵向受拉钢筋的应力或等效应力采用简化的内力臂计算公式计算。梁的刚度是基于弯矩曲率的双折线假定,利用试验资料求出 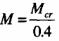 时的刚度降低系数β0.4的拟合近似值,再利用几何关系导出M = Mk时综合刚度的近似计算公式。 时的刚度降低系数β0.4的拟合近似值,再利用几何关系导出M = Mk时综合刚度的近似计算公式。
规范的这种方法,具有下述几点不足之处:
1、简化的内力臂计算公式没有正确地反映内力臂与有关参数的函数关系。根据开裂截面弹性理论计算公式导出的高精度简化式[1]知,内力臂与KS及rs二个参数成线性关系,与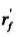 不成线性关系(Ks为纵向受拉钢筋换算截面重心至受拉边缘的距离与h的比值,rs为受拉钢筋换算面积与bh的比值, 不成线性关系(Ks为纵向受拉钢筋换算截面重心至受拉边缘的距离与h的比值,rs为受拉钢筋换算面积与bh的比值,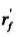 为受压翼缘截面面积与bh的比值)。而规范公式的内力臂与 为受压翼缘截面面积与bh的比值)。而规范公式的内力臂与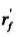 成线性关系,与ks和rs二个参数无关。 成线性关系,与ks和rs二个参数无关。
2、规范的方法只能计算纵向受拉钢筋重心处的截面平均应变值,不能计算其它部位,特别是最大裂缝宽度所在部位,即截面受拉边缘处的平均应变值。而在实际工程中,最大裂缝宽度往往由外观及人们心理上的安全感决定,所以往往需要计算截面受拉边缘处的平均应变值。
3、刚度计算虽然基于双折线假定,但并不是直接利用双折线的规律进行计算,而是引进β0.4的近似拟合值进行计算。由于试验资料的局限性,该值的计算式并没有正确反映该值与有关参数的函数关系。
4、截面平均应变和刚度是一个统一体,但是规范方法没有把二者有机地结合起来,而是分割开来单独计算。
5、钢筋混凝土受弯构件与部分预应力混凝土受弯构件属于同一系列,钢筋砼受弯构件可视为预应力度为零的部分预应力受弯构件,但规范采用了不同的计算公式。
6、对于多次加荷的受弯构件,当所加荷载小于以前曾施加过的最大荷载时,其截面平均应变和刚度的计算将与一次加荷时不同,而且截面平均应变值较一次加荷时大得很多。规范没有提供这种情况下的计算公式。
本文提出的计算方法可以克服规范方法的上述缺点。
部分预应力梁开裂以后截面平均应变和刚度的直接计算法
项剑锋 硕士、教授级高级工程师
(浙江省建筑科学设计研究院、浙江剑锋加固工程有限公司)
提 要:本文基于截面平均应变符合平截面假定,截面弯矩与受拉边缘处平均应变及截面曲率与受拉边缘处平均应变的双折线关系,利用部分预应力梁开裂以后不考虑受拉砼作用时截面上的弯矩—曲率—应变的简化线性关系式,直接导出了开裂以后考虑受拉砼作用时截面平均应变和刚度的精度很高又很简捷的计算公式,并通过计算例题使计算方法更加明了。
关键词:弯矩、曲率、截面平均应变、双折线、刚度、直接计算、计算例题 1 前言
在作预应力梁和钢筋混凝土梁的挠度和裂缝宽度验算时,主要的计算内容是开裂以后的截面平均应变和刚度。由于截面开裂以后,裂缝之间和裂缝顶部的受拉区混凝土还要承担一部分拉力,而这部分拉力的大小和在加荷过程中的衰减速度均受许多因素影响,所以使得开裂以后的截面平均应变和刚度计算变得较为困难。
我国现行混凝土结构设计规范(GB50010-2002)采用将裂缝截面上纵向受拉钢筋的应力(钢筋混凝土梁)或等效应力(预应力混凝土梁)除钢筋弹性模量乘应变不均匀系数的方法计算钢筋重心处的截面平均应变值。裂缝截面上纵向受拉钢筋的应力或等效应力采用简化的内力臂计算公式计算。梁的刚度是基于弯矩曲率的双折线假定,利用试验资料求出 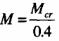 时的刚度降低系数β0.4的拟合近似值,再利用几何关系导出M = Mk时综合刚度的近似计算公式。 时的刚度降低系数β0.4的拟合近似值,再利用几何关系导出M = Mk时综合刚度的近似计算公式。
规范的这种方法,具有下述几点不足之处:
1、简化的内力臂计算公式没有正确地反映内力臂与有关参数的函数关系。根据开裂截面弹性理论计算公式导出的高精度简化式[1]知,内力臂与KS及rs二个参数成线性关系,与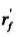 不成线性关系(Ks为纵向受拉钢筋换算截面重心至受拉边缘的距离与h的比值,rs为受拉钢筋换算面积与bh的比值, 不成线性关系(Ks为纵向受拉钢筋换算截面重心至受拉边缘的距离与h的比值,rs为受拉钢筋换算面积与bh的比值,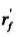 为受压翼缘截面面积与bh的比值)。而规范公式的内力臂与 为受压翼缘截面面积与bh的比值)。而规范公式的内力臂与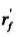 成线性关系,与ks和rs二个参数无关。 成线性关系,与ks和rs二个参数无关。
2、规范的方法只能计算纵向受拉钢筋重心处的截面平均应变值,不能计算其它部位,特别是最大裂缝宽度所在部位,即截面受拉边缘处的平均应变值。而在实际工程中,最大裂缝宽度往往由外观及人们心理上的安全感决定,所以往往需要计算截面受拉边缘处的平均应变值。
3、刚度计算虽然基于双折线假定,但并不是直接利用双折线的规律进行计算,而是引进β0.4的近似拟合值进行计算。由于试验资料的局限性,该值的计算式并没有正确反映该值与有关参数的函数关系。
4、截面平均应变和刚度是一个统一体,但是规范方法没有把二者有机地结合起来,而是分割开来单独计算。
5、钢筋混凝土受弯构件与部分预应力混凝土受弯构件属于同一系列,钢筋砼受弯构件可视为预应力度为零的部分预应力受弯构件,但规范采用了不同的计算公式。
6、对于多次加荷的受弯构件,当所加荷载小于以前曾施加过的最大荷载时,其截面平均应变和刚度的计算将与一次加荷时不同,而且截面平均应变值较一次加荷时大得很多。规范没有提供这种情况下的计算公式。
本文提出的计算方法可以克服规范方法的上述缺点。
2 弯矩与曲率关系曲线的双折线假定
大量的试验资料已表明,部分预应力砼梁和钢筋砼梁在受拉钢筋屈服以前,截面的弯矩—曲率关系曲线可以近似成双折线关系,双折线转折点处的弯矩值为开裂弯矩Mcr(如图1所示)。本文提出的截面平均应变和刚度的计算方法将基于这个关系,即假定所研究的梁截面在使用荷载阶段,其M-Ф关系曲线具有双折线关系。
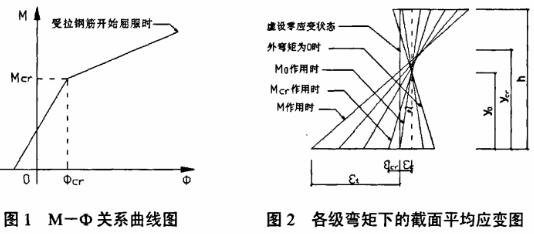
我们知道,弯矩-曲率曲线是根据试验梁在各级弯矩下的截面平均应变的量测值画出来的。双折线M-Φ关系曲线的假定,实际上是将各级弯矩下的截面平均应变假定为如图2所示。其特点是:当弯矩小于Mcr时,应变图均相交于一点;当弯矩大于Mcr时,应变图均相交于较高的另一点。较低的交点处即为开裂以前换算截面形心轴的位置,较高的交点处可以视为开裂以后的换算截面形心轴的位置。
3 截面平均应变和刚度的计算公式 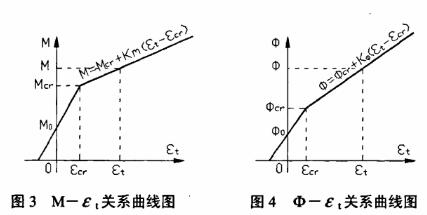
如果把图2画成M-εt关系曲线和Φ-εt关系曲线(εt为截面受拉边缘处的平均应变),可以得到如图3和图4所示的双折线关系。第一段直线可根据未开裂截面的几何特征确定。双折线法的关键是要确定第二段直线。如果能够求得第二段直线的斜率,则任意一个M-Φ-εt的对应值都可以计算,从而截面上任意部位的平均应变值就可以确定;而M-εt直线的斜率除Φ-εt直线的斜率即为开裂以后的截面刚度,所以求得斜率以后也就可以同时求得刚度。因此,本文的主要任务是研究第二段M-εt直线和Φ-εt直线斜率的计算公式。
设第二段M-εt直线和Φ-εt直线的斜率分别为Km和KΦ,则直线的方程分别为:
M = Mcr+Km (εt-εcr) (3-1)
Φ=Φcr+KΦ (εt-εcr) (3-2)
由(3-1)式知:
εt =εcr+(M-Mcr)/ Km (3-3)
根据(3-3)和(3-2)式求得εt和Φ以后,可利用图5中的几何关系,求出截面上至受拉边
缘距离为ax的任意部位处的平均应变值εx :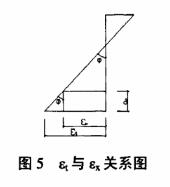
εx = εt- ax·Φ (3-4)
开裂以后的截面刚度Bcr可以按下式计算:
Bcr = Km / KΦ (3-5)
上述(3-2)~(3-5)式便是开裂以后截面平均应变和刚度的计算公式。
4 有关参数的计算公式
4.1、Km和KΦ的计算公式
由图3和图4知,只要能够再定出第二段M-εt直线和Φ-εt直线上的任意一点,Km和KΦ值便可以计算。
我们知道,随着外弯矩的增大,钢筋所承受的拉力不断增大,受拉区混凝土所承受的拉力在截面总拉力中所占的比例越来越小,它对截面应变的约束作用也越来越弱。如果假定在任意大荷载作用下受压区混凝土和截面上的纵向钢筋都不会产生塑性变形,即假定砼的抗压强度和纵向钢筋的屈服强度均无限高,则当截面应变增大到某一程度时,受拉区混凝土所起的作用便可以忽略不计。以弯矩与截面受拉边缘应变的关系曲线为例,双折线化的M-εt实测直线和按开裂截面弹性理论计算公式(即不考虑受拉混凝土作用)计算得到的M-εt关系曲线如图6所示。二者之间的应变差值即为受拉区混凝土的作用。随着弯矩的增大,二者的差距越来越小。由于假定受压区砼和截面上的纵向钢筋都不会产生塑性变形,所以随着外弯矩的增加,二者将沿着直线的延长线上升,相交于Sˊ点(如图6所示)。Sˊ点处的应变值即为可以忽略受拉区混凝土作用时的应变值。
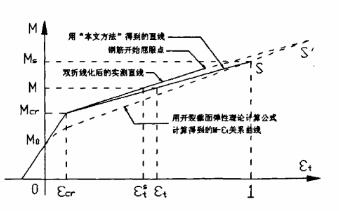
如果知道Sˊ点处的应变值,便可以根据文献[1]中的简化计算公式计算Sˊ点处的弯矩值和曲率值,于是便可以求出Km和KΦ值。因此,问题的关键是要确定Sˊ点处的应变值。
通常的做法是以受拉钢筋开始屈服时的应变值作为Sˊ点处的应变值,如文献[2]的做法。但是试验资料表明,这种做法对于配置屈服强度较低钢筋的梁截面误差较大,因为当钢筋开始屈服时受拉区混凝土的作用仍比较显著,而且这种做法计算不方便,使公式中多了一个钢筋屈服应变的参数。
为了简化计算,本文统一以εt = 1作为Sˊ点处的应变值,即以S点代替Sˊ点(如图6所示)。实际上,当εt = 1时,钢筋早已屈服,受压区砼早已破坏,所以S点并不存在,它是在假定受压区混凝土和截面上的纵向钢筋的强度均无限高的条件下得到的。
设截面受拉边缘处应变εt = 1时所相应的外弯矩值为Ms,截面曲率为Φs,则Km和KΦ可以由下列公式求得:
Km = (Ms -Mcr) / (1-εcr)
KΦ = (Φs-Φcr) / (1-εcr)
由于εcr﹤﹤1,Mcr﹤﹤Ms ,Φcr﹤﹤Φs ,所以可得:
|
Km = Ms |
(4-1) |
|
KΦ =Φs |
(4-2) |
4.2、Φs和Ms的计算公式:
对于图7所示的T形截面,文献[1]基于开裂截面弹性理论导出了部分预应力梁开裂以后截面上的弯矩—曲率—应变的精确关系式,并借助电子计算机对各种情况下的截面作了分析,进而得出了精度很高(一般情况下误差不大于5%)的弯矩—曲率—应变的简化线性关系式。其表达式如下(已将原式中的RβΦ改为RΦ、Rβm改为Rm):
Φ=(R0Φ·ε0+RΦ·εt)/ h
M = NP0(R0m·h-aN)+(0.85EcA0h)·Rm·εt
式中εt—截面受拉边缘处的截面平均应变值;
NP0—混凝土法向预应力等于零时预应力钢筋及
非预应力钢筋的合力;
aN—NP0至截面受拉边缘的距离;
ε0—开裂前换算截面形心轴处的应变值。
R0Φ、、RΦ和R0m、Rm为计算系数,可查表计算。
将εt = 1代入上式,得
Φs = (R0Φ·ε0+RΦ)/ h
Ms = NP0(R0mh-aN)+(0.85EcA0h)·Rm
由于R0Φ·ε0﹤﹤RΦ NP0(R0mh-aN)﹤﹤(0.85EcA0h)·Rm
所以Φs和Ms可按下式计算:
|
Φs = RΦ/ h |
(4-3) |
|
Ms = (0.85EcA0h)·Rm |
(4-4) |
4.3、Rm、RΦ的计算公式:
根据文献[1]的研究结果,Rm和RΦ可按下列公式计算(已将原式中的Rβ0m、Rrsm、Rksm和
Rβ0Φ、RrsΦ、RksΦ改为R1m、R2m、R3m和R1Φ、R2Φ、R3Φ):
|
RΦ = R1Φ+(R2Φ-R3Φ·Ks)γs |
(4-5) |
|
Rm = R1m+(R2m-R3m·Ks)γs |
(4-6) |
式中的R1m、R2m、R3m和R1Φ、R2Φ、R3Φ可直接从表1中查得。 式中的Ks为受拉区的预应力钢筋和非预应力钢筋总换算面积的形心至受拉边缘的距离与截面高度h的比值。
式中的γs为受拉区的预应力钢筋和非预应力钢筋总换算面积与bh的比值。
RØ和Rm都有明确的物理意义:
Rm——开裂截面的截面抵抗矩系数:
RØ——开裂截面的形心轴位置系数:
Rm / RØ——开裂截面的刚度系数。
表1 计算系数查用表
|
系数
γfˊ |
R1m |
R2m |
R3m |
R1Φ |
R2Φ |
R3Φ |
|
0 |
0.0142 |
0.644 |
1.85 |
1.250 |
3.12 |
5.1 |
|
0.1 |
0.0118 |
0.629 |
1.69 |
1.184 |
2.62 |
4.0 |
|
0.2 |
0.0100 |
0.604 |
1.55 |
1.147 |
2.23 |
3.2 |
|
0.3 |
0.0082 |
0.576 |
1.43 |
1.126 |
1.94 |
2.7 |
|
0.4 |
0.0072 |
0.547 |
1.32 |
1.112 |
1.70 |
2.3 |
|
0.5 |
0.0063 |
0.521 |
1.24 |
1.104 |
1.51 |
2.0 |
|
0.6 |
0.0054 |
0.495 |
1.16 |
1.096 |
1.35 |
1.7 |
|
0.7 |
0.0050 |
0.470 |
1.08 |
1.092 |
1.22 |
1.5 |
|
0.8 |
0.0045 |
0.448 |
1.02 |
1.089 |
1.12 |
1.4 |
|
0.9 |
0.0044 |
0.429 |
0.98 |
1.088 |
1.03 |
1.3 |
|
≥1.0 |
0.0043 |
0.409 |
0.92 |
1.088 |
0.95 |
1.2 |
注:γfˊ为受压区翼缘挑出部分面积及受压区的预应力钢筋和非预应力钢筋的换算面积总和与bh的比值;当γfˊ处于表列数值之间时,可采用线性插值法。
4.4、ε0 、M0和εcr 、Φcr、Mcr的计算公式:
1)、ε0的计算
ε0是开裂前换算截面形心轴处的应变值,按下式计算:
ε0 = Npo/(0.85EcA0) (4-7)
2)、M0的计算
M0是使截面受拉边缘的应力为0时所需的外弯矩值,可按下式计算:
M0 = Npo /(W0/A0+Y0-aN) (4-8)
3)、εcr的计算
εcr是相应于Mcr作用时,把截面受拉区混凝土折算成完全弹性材料后受拉边缘处的应变值。由于受拉区混凝土在截面即将开裂时出现显著的塑性变形,所以这是为了方便计算所虚设的值。按我国现行规范(GB50010-2002)的方法,εcr的计算公式如下:
εcr = γ·ftk /(0.85Ec) (4-9)
式中γ为截面抵抗矩塑性影响系数,按规范8·2·4条计算。
4)、Φcr的计算
Φcr是相应于Mcr作用时的截面曲率值。它也是为了方便计算所虚设的值。由图2可以看出,Φcr可以按下式计算:
Φcr =(εcr+ε0)/ Y0 (4-10)
5)、Mcr的计算
Mcr为正截面开裂弯矩值,计算公式为:
Mcr = M0+γ·ftk·W0 (4-11)
5 工字形截面计算公式的探讨
上述计算公式是根据T形截面建立起来的。对于工字形截面,由于比T形截面多出了受拉翼缘挑出部分面积,使得截面开裂以前的刚度及开裂弯矩有较大增加。在截面开裂后,由于受拉翼缘退出工作,其受力性能逐渐与T形截面接近。其弯矩—曲率曲线如图8所示。
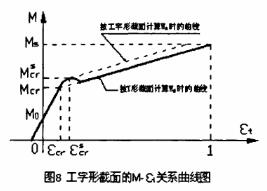
如何将工字形截面的弯矩—曲率曲线简化成双折线,是一个需要作进一步探讨的的问题。
在计算Φs和Ms时,由于受拉翼缘已退出工作,即使中和轴还处于下翼缘内,也由于中和轴附近的应变很小,而可以忽略受拉翼缘挑出部分混凝土面积所承担的压力,因而可以按T形截面计算。
在计算εcr 、Φcr和Mcr时,如果按工字形截面考虑,则第二段直线将如图8中的细虚线所示,显然与实际曲线偏差较大,而且裂缝宽度和挠度的计算值将偏小,不安全。为了减小偏差并偏于安全考虑,笔者建议在按(4-11)式计算Mcr时,W0值按T形截面计算,不考虑受拉翼缘的作用。
|
6 多次加荷时的计算方法

M-Ф的双折线关系只适用于一次加荷的情况。当开裂以后,从某一荷载值卸荷并再次加荷时,M-Ф曲线将近似呈三折线关系(如图1所示)。第一个转折点处的弯矩值为截面受拉边缘应变为零时的弯矩值M0,第二个转折点处的弯矩值为以前曾作用过的荷载所产生的最大弯矩值Mmax,第一阶段直线和第三阶段直线均跟一次加荷时的情况基本吻合。其M-εt关系曲线和Ф-εt关系曲线如图9和图10所示。
设M-εt关系曲线的第2段和第3段直线的斜率为Km2和Km3 ;设Ф-εt关系曲线的第2段和第3段直线的斜率为KФ2和KФ3 。由于第1段和第3段直线均跟一次加荷时的双折线关系曲线重合,所以Km3和KФ3及M≥Mmax以后的截面平均应变εx均可以利用一次加荷时的计算公式计算。而Km2和KФ2则可以利用图中的几何关系计算。公式为:
|
εmax = εcr+(Mmax-Mcr) / Km3 |
(6-1) |
|
Фmax = Фcr+KФ3(εmax-εcr) |
(6-2) |
|
Ф0 = ε0 / Y0 |
(6-3) |
|
Km2 = (Mmax-M0) /εmax |
(6-4) |
|
KФ2 = (Фmax-Ф0) /εmax |
(6-5) |
求得Km2和KФ2以后,便可以利用下述式子求M0﹤M﹤Mmax时截面底边的平均应变和曲率:
|
εt = (M-M0)/ Km2 |
(6-6) |
|
Ф = Ф0+KФ2·εt |
(6-7) |
求得εt和Ф以后,可以利用下式求截面上至受拉边缘距离为ax的任意部位处的平均应变εx:
截面开裂后的刚度B2按下述式子计算:
当上述方法用于实际工程时,还需要确定Mmax值。 |
7 截面平均应变和刚度的计算公式汇总
(一)7.1、一次加荷时
|
γfˊ = [(bfˊ-b)hfˊ+npˊ·Apˊ+nsˊ·Asˊ]/ bh |
(7-1) |
|
γs = (np·Ap+ns·As)/ bh |
(7-2) |
|
Ks = (np·Ap·ap+ns·As·as)/[( np·Ap+ns·As)·h] |
(7-3) |
|
Rm = R1m+(R2m-R3m·Ks)·γs |
(7-4) |
|
RФ = R1Ф+(R2Ф-R3Ф·Ks)·γs |
(7-5) |
|
ycr = h / RФ≦h-hfˊ |
(7-6) |
若ycr﹥h-hfˊ,则应按b = bfˊ的矩形截面重新计算。
|
ε0 = Np0 /(0.85EcA0) |
(7-7) |
|
εcr = (γ·ftk)/ 0.85Ec |
(7-8) |
|
Ф0 =ε0 / Y0 |
(7-9) |
|
Фcr = (ε0+εcr)/ Y0 |
(7-10) |
|
M0 = Np0(W0 / A0+y0-aN) |
(7-11) |
|
Mcr = M0+γ·ftk·W0 |
(7-12) |
|
Wcr =Rm·A0h |
(7-13) |
|
εt =εcr+(M-Mcr)/( 0.85Ec Wcr) |
(7-14) |
|
Ф = Фcr+(εt-εcr)/ Ycr |
(7-15) |
|
εx =εt-ax·Ф |
(7-16) |
|
B3 = 0.85Ec·Wcr·Ycr |
(7-17) |
(二)7.2、多次加荷时
|
εmax =εcr+(Mmax-Mcr)÷(0.85Ec·Wcr) |
(7-18) |
|
Фmax = Фcr+(εmax-εcr)/ ycr |
(7-19) |
|
εt = (M-M0)÷(Mmax-M0)·εmax |
(7-20) |
|
Ф = Ф0+εt /εmax·(Фmax-Ф0) |
(7-21) |
|
εx = εt-ax·Ф |
(7-21) |
|
B2 = (Mmax-M0)÷(Фmax-Ф0) |
(7-22) |
8 计算例题
截面形状和尺寸如图11所示。已知使用阶段时截面上所有钢筋在砼法向预应力等于零时的合力Np0 = 857KN;砼、预应力钢筋和非预应力钢筋的弹性模量分别为Ec = 3.25×104N/mm2、Ep = 1.95×105N/mm2、Es = 2×105N/mm2;砼的标准抗拉强度ftk = 2.39 N/mm2。试计算:初次加荷和多次加荷M = 700KN·m时,截面底面和非预应力钢筋重心处的截面平均应变值,及截面开裂以后受拉钢筋屈服以前在初次加荷和多次加荷时的刚度。设该截面曾作用过的最大弯矩值为M*max = 840KN·m。
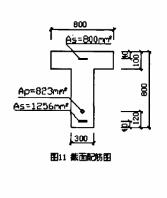
[解]
1、 求截面几何特征值和基本计算量:


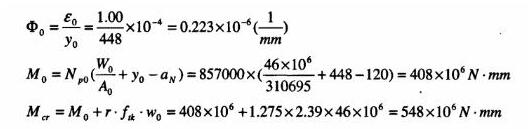
2、根据γfˊ= 0.232由表1查计算系数,查得:
R1Ф = 1.140 R2Ф = 2.14 R3Ф = 3.0
R1m = 0.0094 R2m = 0.595 R3m = 1.51
3、求RФ和Rm:
RФ = R1Ф+(R2Ф-R3Ф·Ks)γs = 1.140+(2.14-3.0×0.089)×0.062 = 1.256
Rm = R1m+(R2m-R3m·Ks)γs = 0.0094+(0.595-1.51×0.089)×0.062 = 0.0380
4、求Фs和Ms :
Фs = RФ/ h = 1.256÷800 = 0.00157
Ms = (0.85EcA0h)·Rm = 0.85×3.25×104×310695×800×0.0380 = 0.26×1012 N·mm
5、检验中和轴位置:
Kh = 1/Фs = 1/0.00157 = 637mm﹤800-100 = 700mm
中和轴尚未上升到受压区内
6、求Km3和KФ3 :
Km3 = Ms = 0.26×1012N·mm
KФ3 = Фs = 0.00157(1/mm)
7、求初次加荷M = 700KN·m时截面底部和非预应力钢筋重心处的平均应变εt和εs :
εt = εcr+(M-Mcr)/ Km3
= 110×10-6+(700×106-548×106)÷(0.26×1012) = 695×10-6
Ф = Фcr+KФ3(εt-εcr)
= 0.469×10-6+0.00157×(695-110)×10-6 = 1.39×10-6(1/mm)
εs =εt-as·Ф = 695×10-6-40×1.39×10-6 = 639×10-6
8、求初次加荷开裂以后的刚度B3 :
B3 = Km3 / KФ3 = 0.26×1012÷0.00157 = 166×1012N·mm
9、求多次加荷M = 700KN·m时的εt和εs :
εmax =εcr +(Mmax-Mcr) / Km3
= 110×10-6+(840-548)×106÷(0.26×1012) = 1233×106
Фmax = Фcr+KФ3(εmax-εcr)
= 0.469×10-6+ 0.00157×(1233-110)×10-6 = 2.23×10-6
Km2 = (Mmax-M0) /εmax
= (840-408) ×106÷(1233××10-6) = 0.35×1012
KФ2 = (Фmax-Ф0) /εmax
= (2.23-0.223) ×10-6÷(1233××10-6) = 0.00163
εt = (M-M0) / Km2 = (700-408)×106÷(0.35×1012) = 834×10-6
Ф = Ф0+KФ2·εt = 0.223×10-6+0.00163×834×10-6 = 1.58×10-6(1/mm)
εs = εt-as·Ф = 834×10-6-40×1.58×10-6 = 771×10-6
10、求开裂以后多次加荷时的刚度B2 :
B2 = Km2 / KФ2 = 0.35×1012÷0.00163 = 215×1012N·mm
9 结束语
本文基于截面平均应变符合平截面假定,截面弯矩与受拉边缘处平均应变及截面曲率与受拉边缘处平均应变的双折线关系,利用部分预应力梁开裂以后不考虑受拉混凝土作用时截面上的弯矩—曲率—应变的简化线性关系式,直接导出了开裂以后考虑受拉混凝土作用时截面平均应变和刚度的计算公式。这些计算公式除了形式简单、计算工作量少外,还具有下述特点:
1、由于简化计算式正确地反映了截面弯矩、曲率、应变与各有关参数的函数关系,所以计算结果的精度较高;
2、所建立的公式不仅对部分预应力受弯构件适用,对钢筋混凝土受弯构件和大偏心受压构件也适用;
3、可以计算截面上任意部位的截面平均应变值,因而可以计算截面任意部位处的裂缝宽度值;
4、可以同时计算截面平均应变和刚度,使得裂缝宽度计算和挠度计算连成一体;
5、不仅可以计算一次加荷时的截面平均应变和刚度,还可以计算多次加荷时的截面平均应变和刚度,符合构件的实际使用情况。
参考文献
[1] 项剑锋:“部分预应力梁不考虑受拉混凝土作用时截面应变的计算”,《建筑结构学报》,1983年第4期,P34~45。
[2] R.F.Warner,“Serviceability of Cracked Prestressed Concrete Members: Tests and Analysis”。FIP Symposia onPartial Prestressing .1980. Bucharest. Romania, Procedings : Part I. |