对于上述问题采用传统的深度优先策略时，搜索树如图1所示，为了简化绘图，只给出n=3，m=3的情况。若能与规则匹配的是 S_=[G12, G22, G32]，则要经过14次搜索才能搜索到目标，最坏情况下要搜索33=27次。

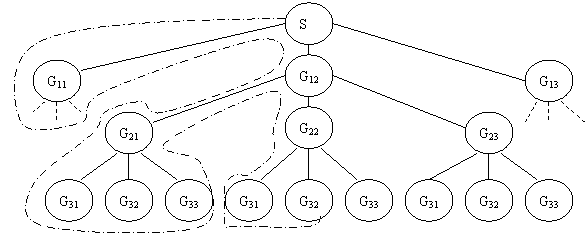
图1  相关对象组合按深度优先搜索

如果我们能够解除对象之间的相关关系，相当于把规则中的变量都改为常量，即实现解耦，如图2所示，问题将大为简化。

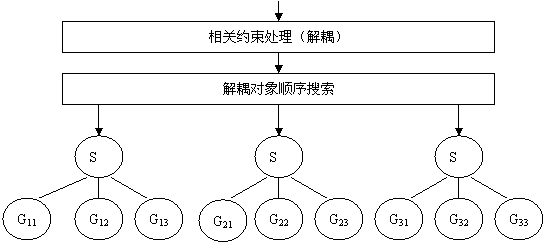
图2  相关对象组合的解耦递解智能搜索

这里，解耦处理后的搜索已变成三个独立的搜索。若机器不能并行处理，最坏的情况下也只要搜索3×3=9次。当n和m取更大值时，开销的减少更显著，从nm次减为n m次。本文提出“闭环消除法”，先将相关关系写入规则，然后消去不满足相关约束的那些数据，剩下的全部满足相关约束。匹配时就只需考虑数据中那些已知常量的匹配，也就实现了解耦，只需顺序搜索了。由于消去一些数据，顺序搜索次数也更少一些。

3  闭环消除法算法

（1） 按闭环消除法处理相关约束时，我们将规则T和对象G1～Gm中的数据都构成闭环，如图3所示。

（2）引入规则知识作为搜索引导：对T_ 中的x、y、z用xij、yij、zij代替。这里，字符i,j指明：T_中的本位字符应与后面邻近Ti中的第j位字符相等（即相关约束条件）。例如，在（4）式T1中的x就写作x43，T4中的x则写作x56，T5中的x则写作x12 。

（3）对第一个变量 x 执行消除法：在规则闭环中，找到第一个出现xij 的项 Tp，然后对Gi 中的n个数据逐个判断，若能在前一项Gp 的n个数据中搜寻到一个数据，其中的g pq = g ij ，则将Gi 的这个数据保留，否则消去。这一过程从G1到Gm往后推进，凡遇有变量x就按此处理，否则保留全部数据。

（4）第二次执行数据的闭环消除：当处理进行到Gm后，还不能保证把全部不满足相关约束的数据消去。这时，按图3再返回到G1，把已得到的信息（即经消除处理后在最后一个相关对象中保留下来的数据）反馈到起始点处。再作消除工作，往下进行，到Gm-1为止。

（5）对其余变量进行闭环消除工作： x 变量的消除完成后，再对y、z照样进行。当对一个变量进行消除工作时，权把其它变量当作常量。

（6）自动生成子规则：在对象知识库中对x，y，z 搜索到满足相关约束条件的代码后，用这些已知代码替换x，y，z，于是规则中全是常量，解除了耦合。若搜索得到多个结果，则将形成多条子规则。 

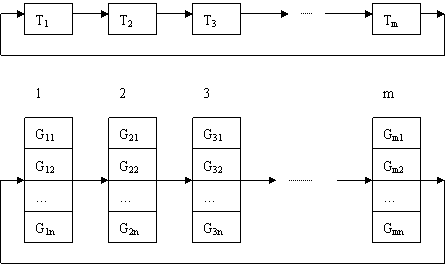
图3  闭环消除法

   将以上方法用于第2节的英文句子时，先将T3中的x用x42 ，T4 中的x用x34代替。对x执行消除法只涉及规则和对象的两个项，在电子词典的相应位置搜索到 g34 = g 42 = 9（表示性质的代码），将规则T中的x 换作9。对y 的操作也类似，不赘述。

4         闭环消除法的证明

命题：采用闭环消除法处理模型1问题后，在所有相关对象中若还剩余数据，则它们全部满足全局相关约束条件。

   证明：

我们先讨论对某一相关参数（如x）作消除工作。

设问题中的相关对象(相对于x)依次为Gi、Gj、Gk、… Gs、Gt，。从Gi出发，对Gj进行消除处理后，则Gj中剩余的全部数据定能在Gi中找到相应的数据，使它们之间满足局部相关约束（因为不相关的数据已经消去）。我们把这一特性称作相关包含（意指满足局部相关的数据包含在Gi的若干数据中），用符号 ∝ 表示，记作

Gj ∝ Gi                                （7）

上一页  [1] [2] [3]  下一页